Идентификация факторов риска

Задание 1

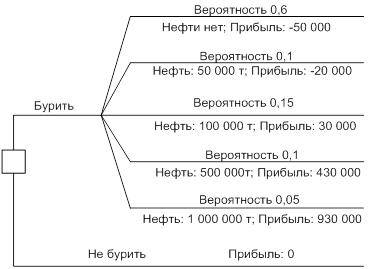
Нефтедобывающая компания решает вопрос о бурении скважины. Вероятность успешности бурения, объёмы добычи и экономический результат представлены в таблице:

Построить дерево решений вопроса о бурении скважины для компании. Построить функцию полезности для данного выбора (предполагается, что руководство компании безразлично к риску), определить полезность по вариантам решений.

Принять максимальную полезность равной 100 U (utility), U – условная единица полезности.

Решение:

Ожидаемое значение выигрыша составит:

0,6 (-50 000) + 0,1 (-20 000) + 0,15 * 30 000 + 0,1 * 430 000 + 0,05 * 1 000 000 = 62000 тыс. у.е.

Если ЛПР, представляющее фирму, безразлично к риску и принимает решение о проведении буровых работ на основании рассчитанного значения выигрыша, то оно воспринимает ожидаемую полезность как пропорциональную ожидаемому значению.

В этом случае функция полезности U (v), где v – прибыль, получаемая при различных исходах, является прямой с положительным наклоном.

Значения полезностей могут быть найдены за два шага:

1. Присваиваются произвольные значения полезностей выигрыша для лучшего и худшего исходов, причем первой величине ставится в соответствие меньшее число.

U (-50 000) = 0, а U (930 000) = 100

Тогда полезности промежуточных выигрышей будут находится в интервале от 0 до 100.

2. Игроку предлагается на выбор: получить некоторую гарантированную денежную сумму v, находящуюся между лучшим и худшим значениями S и s, либо принять участие в игре, т.е. получить (1 – p) – наименьшую сумму. При этом вероятность следует изменять (повышать или понижать) до тех пор, пока ЛПР станет безразличным в отношении к выбору между получением гарантированной суммы и игрой. Пусть указанное значение вероятности равно p0. Тогда полезность гарантированной суммы определяется как среднее значение полезностей наименьшей и наибольшей сумм, т.е.:

U (v) = p0 U (S) + (1 – p0) U (s).

Пусть для ЛПР безразлично, потерять 20000 тыс. у.е. или принять участие в игре (выигрыш 930 000 тыс. у.е. с вероятностью 0,1 или проигрыш 50 000 тыс. у.е. с вероятностью 0,9.

U (-20) = 0,1 U (930) + 0,9 U (-50) = 0,1 * 100 + 0,9 * 0 = 10.

Задание 2

В банк представлено шесть инвестиционных проектов, которые характеризуются следующими итоговыми показателями: